Цифры

Цифры по их происхождению представляют собой семантические логограммы, а по применению  идеограммы (…); они служат для краткого обозначения чисел и используются (в отличие от словесной записи чисел) главным образом для математических вычислений. Слово ««цифра» происходит от арабского sifra  «пустота» и первоначально обозначало нуль.

История цифр изучалась главным образом в двух отношениях: в работах по истории математики и ню теории чисел, в которых история цифр рассматривалась лишь попутно; в работах по палеографии, в которых основное внимание уделялось графике цифр, причем, как правило, в пределах какой-либо одной системы письма. История цифр как особых письменных знаков, образующих системы, принципы построения которых связаны с принципами построения различных типов письма, изучена недостаточно.

Основные особенности цифр следующие. Во-первых, в отличие от обычных письменных знаков, которые применяются для записи любой речи, цифры имеют более узкое назначение; они служат для краткой записи чисел. Во-вторых, все цифры  от древнейших и до современных  являются по их происхождению семантическими логограммами; цифра обозначает целое слово (имя числительное). Такой характер цифр создает возможность более компактного обозначения чисел, делает цифры удобными для математических операций и облегчает их международное применение.

[506]

Почти все цифровые системы строились по десятичному принципу (едва ли не единственное исключение  системы майя и ацтеков с их пятирично-двадцатиричным принципом); это объяснялось тем, что древнейшим орудием счета были две руки с их десятью пальцами. Десятичный принцип иногда дополнялся пятиричным (например, греческая аттическая, римская и другие цифровые системы), двадцатиричным (например, финикийская система) и даже шестидесятиричным (у вавилонян) и двенадцатиричным (в счете дюжинами). Пятиричный принцип исходил из количества пальцев на одной руке, двадцатиричный  из количества пальцев на руках и ногах; шестидесятиричный возник у вавилонян в связи с их весовыми единицами; происхождение двенадцатиричного принципа связано с тем, что число 12 имеет много сомножителей  2, 3, 4, 6.

Другая особенность почти всех цифровых систем в том, что самостоятельные знаки имелись в них лишь для простейших чисел: количество таких знаков колебалось от 45 до 30. Все остальные числа получались по принципу сложения (например, в римской системе число 6  сложением знаков «пять» и «один» = VI, в «арабской»  число 23  сложением цифр 20 и 3); крупные числа иногда получались по принципу умножения (например, в греческой ионической системе над знаком «десять тысяч» ставился знак «три», что значило «тридцать тысяч»); реже применялся принцип вычитания (например, римские цифры IV, IX); ни в одной из цифровых систем не использовался принцип деления.

Большим, но поздним достижением в истории цифр было применение «позиционного принципа», согласно которому числовое значение цифровых знаков зависит не только от их формы, но и от места по отношению друг к другу (например, римские цифры IV и VI, арабские 16 и 61). Развитие позиционного принципа обусловило появление знака нуль, обозначающего отсутствие числа.

Развитие цифр связано с общим развитием письма.

На ранней пиктографической ступени письма цифр еще не существовало. В случаях обозначения числа предметов рисовали эти предметы, повторяя их изображение нужное количество раз; так, в пиктограмме на рис. 2, б двухмесячная продолжительность похода передавалась изображением двух лун. Позже появился более сложный способ: рисовали предмет, о котором шла речь, а рядом ставили точки или черточки, количество которых указывало число (рис. 1, а; 2, б). Использовался этот способ и в недавнее время; так, на русских монетах начала XIX века наряду с цифрой ставились точки, пояснявшие неграмотным стоимость монеты. Такой способ был удобным для передачи небольших чисел,

[507]

применявшихся на ранних ступенях развития общества; точки и черточки послужили прообразом простейших цифровых знаков единиц.

Цифры в их развитой форме, т. е. знаки, обозначавшие не только единицы, но и другие, более крупные числа, появились позже, в древнейших логографических, логографически-звуковых и логографически-слоговых системах.

Появление развитых цифровых знаков было обусловлено необходимостью компактной записи больших чисел, для которой точки и черточки, обозначавшие единицы, были 'непригодны; в свою очередь необходимость записи больших чисел была вызвана развитием торговли и науки в рабовладельческих государствах. В древнейших системах письма цифровые знаки почти не отличались по типу от любых иных логограмм. С этим 'была связана и другая особенность: в более поздних, слоговых и звуковых системах наряду с логографической (цифровой) записью чисел применяется и фонетическая (слоговая или буквенно-звуковая) их запись; в древнейших системах письма числа почти всегда передавались в письме при помощи цифровых логограмм.

Наибольшее значение из древнейших цифровых систем имеют египетская, критская, переднеазиатские клинописные и китайская.

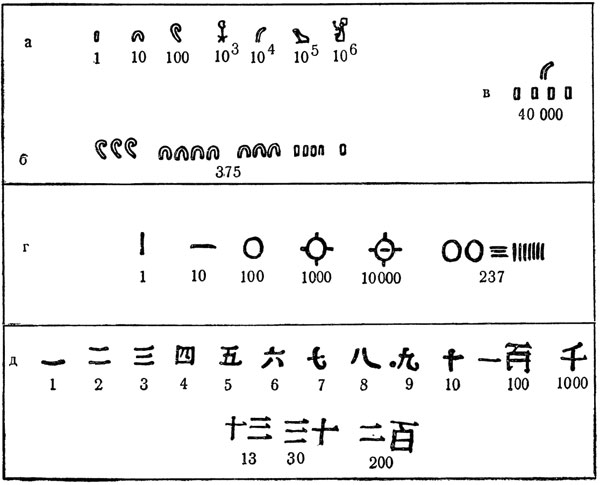
Египетская система была построена на основе строго выдержанного десятичного принципа. Особые знаки имелись только для единицы и различных степеней от числа 10; для «единицы» применялась горизонтальная, реже вертикальная черточка, для «десяти» дуга, для «сотни» свернутая веревка, для «тысячи» стебель папируса, для «десяти тысяч»  согнутый палец, для «сотни тысяч»  головастик (потому что головастики выводятся в очень больших количествах), а для «миллиона»  знак в виде человека, поднявшего руки в изумлении перед таким огромным числом (рис. 144, а). Все остальные числа получались по принципу сложения указанных основных цифр, поставленных рядом; так, для числа 375 повторяли три раза знак «сотни», семь раз  знак «десяти» и пять раз  знак «единицы» (рис. 144, б) 1.

Цифровые знаки начали применяться в Египте еще в додинастическую эпоху, при переходе от пиктографии к логографии; так, в надписи Нармера (конец IV тысячелетия до н. э.) имеются знаки (стебли папируса), которые многими египтологами понимаются как обозначения тысяч (рис. 13). Начиная со «Среднего царства», обозначение крупных чисел строилось не по принципу сложения, а по

____

1. М. А. Коростовцев. Египетская филология. М., 1963, стр. 133.

[508]

принципу умножения; в этом случае крупное число делилось на два сомножителя, меньший из которых (например, единицы) писался под большим (например, под тысячами  рис. 144, в). В иератическом и демотическом письме цифровые знаки приобрели скорописную форму; кроме того, появились особые знаки почти для всех единиц и десятков. В египетских дробях числителем почти всегда была единица (исключение  2/3); так, дробь 4/15 обозначали как сумму 1/5 и 1/15 (папирус Ахмеса, начало II тысячелетия до н. э.). Записывали дроби следующим образом: сверху ставили логограмму «часть» (по-египетски r), а под ней цифровыми знаками указывали, какая именно часть целого имеется в виду; для 1/2 иногда применялась особая логограмма  «сторона», «бок» 2.

Близка к египетской критская система цифр, тоже построенная по десятичному принципу. Особые знаки (рис. 144, г) имелись здесь для «единицы» (вначале точка, позже вертикальная черточка), «десятки» (горизонтальная черточка), «сотни» (круг), «тысячи» (круг с черточками); появился знак и для «десяти тысяч».

При написании числа каждый из знаков повторялся столько раз, сколько было в числе единиц, десятков и сотен; так, при написании числа 237 два раза повторялся знак «сотни» (круг), три раза  знак «десятки» (горизонтальная черта) и семь раз  знак «единицы» (вертикальная черта). Имелись особые обозначения сложения, суммы и т. д.; применялась, согласно А. Эвансу 3, также система процентов.

Близка к египетской (в ее иератически-демотическом варианте) китайская цифровая система (рис. 144, б). Система эта тоже строилась на десятичном принципе; однако особые знаки имелись в ней ее только для единицы и различных степеней от 10, но и для некоторых других чисел (см., например, на рис. 144, д знаки 6, 7, 8, 9). Наряду с принципом сложения знаков применялся принцип умножения; так, число 400 иногда передавалось знаком 100 с надписанными над ним (или влево от него) знаком 4.

Наибольшим своеобразием, сложностью и в то же время использованием передовых принципов счисления отличались переднеазиатские цифровые системы.

Простейшие цифровые обозначения точечного типа встречаются в самых древних шумерских надписях середины IV тысячелетия до н. э. Позднее, в связи с возросшими требованиями хозяйства, цифровые системы Передней Азии переживают быстрое развитие.

____

2. Там же, стр. 135.

3. А. Эванс. Критское линейное письмо. «Вестник древней истории», 1939, №3, стр. 37.

[509]

144. Египетские (а, б, в), критские (г) и китайские (д) цифры с образцами цифровой записи

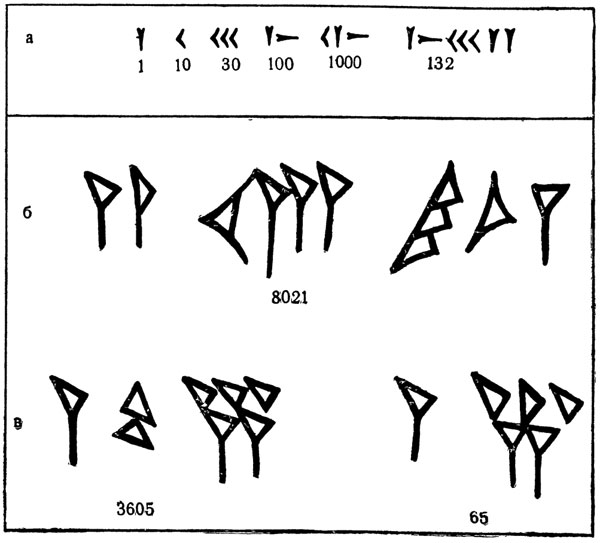
Одна »из этих систем, построенная на десятичном принципе, была сходна с египетской. Система эта имела знаки 4 для «единицы» (вертикальный клин), для «десятки» (вертикальный угол), для «сотни» (вертикальный и горизонтальный клинья) и для тысячи (соединение, как бы умножение знаков «десять» и «сто» - рис. 145, а).

Остальные числа получались по принципу сложения; так, для обозначения числа 132 писали: один раз знак «сотни», три раза знак «десятки» и два раза знак «единицы».

Сложнее была другая система, сочетавшая десятичный принцип с шестидесятиричным. Появление у народов Передней Азии шестидесятиричного принципа счета многие объясняют тем, что этими народами применялись две весовые единицы  шумерская «мина»

_______

4. Здесь и далее указываются те цифровые знаки, которые применялись в Передней Азии после перехода к клинообразному письму; до этого знаки имели иную форму, показанную на рис. 24.

[510]

145. Шумеро-аккадские цифры и их применение а-знаки десятичной цифровой системы; б  десятично-шестидесятиричная цифровая запись с использованием позиционного принципа (2 таланта, 13 мин, 41 шекель); в  десятирично-шестидесятиричная цифровая запись с использованием позиционного принципа и знака разделения  прообраза современного нуля (слева  один талант, вместо мин  знак разделения и пять шекелей, справа  одна мина, пять шекелей)

и аккадский «шекель», причем «мина» была в 60 раз крупнее «шекеля»; позднее возникла также третья единица  «талант», равная 60 «минам». Наличие таких трех единиц, из которых каждая большая равнялась 60 меньшим, привело к тому, что шумеро-аккадская система счета и цифр оказалась построенной на сочетании десятичного и шестидесятиричного принципа. Так, вместо «восемь тысяч двадцать один», говорили: «Два таланта (3600 X 2), тринадцать мин (60 X 13) и сорок один шекель (41)»; соответственно строилась и запись этого числа (145, б). При этом для обозначения и «шекелей», и «мин», и «талантов» применялось два основных знака: вертикальный клин, обозначавший «единицу», и вертикальный угол, обозначавший «десять».

[511]

Такое построение обусловило появление позиционного принципа: значение цифры стало зависеть не только от ее формы, но и от места ее в числовой записи. Так, первый из двух основных знаков этой системы  вертикальный клин  в зависимости от его места в записи мог обозначать: единицу (один «шекель»), 60 (одну «мину») и 3600 (один «талант»); соответственно второй из основных знаков  вертикальный угол  мог обозначать: 10 (десять «шекелей»), 600 (десять «мин») и 36 000 (десять «талантов»). Знаки, обозначавшие «таланты», писали перед знаками «мин», а знаки «мин» перед «шекелями», с отделением каждого из этих разрядов цифр пробелами. Но такая запись чисел оказаласьнеудобной, когда в ней отсутствовал средний разряд («мины»): числа 65 (одна «мина», пять «шекелей») и 3605 (один «талант», пять «шекелей) писались одинаково. Поэтому был введен особый знак разделения (два косых клина, один на другом); знак этот указывал, что в цифровой записи отсутствуют единицы того разряда» на месте которого стоял этот знак (рис. 145,в). Знак этот явился прообразом современного нуля. По особому строились дроби: их знаменатель равнялся 6, 60, 360, 3600, 36 000; так, вместо 1/2 писали 3/6, вместо 2/3-4/6.

Переднеазиатская система цифр (так же как и системы клинописи) была очень сложной. В то же время она оказалась и наиболее прогрессивной из древнейших систем; в ней впервые были применены позиционный принцип и особый знак (прообраз нуля) для обозначения отсутствия данного разряда цифр. Как отмечает В. В. Струве5, пережитки переднеазиатской шестидесятиричной системы сохранились до нашего времени; так, час делится на 60 минут, минута  на 60 секунд, окружность  на 360 градусов.

Особый характер имели системы майя и ацтеков. Системы эти были построены на пятирично-двадцатиричном принципе счета. Особые знаки имелись для «единицы» (точка), «пяти» (черточка), «двадцати» (у ацтеков - знамя). Остальные числа получались повторением (сложением) основных знаков (рис. 16 и 56); например, три черточки и четыре точки == 19. Согласно Ю. В. Кнорозову, майя использовали и позиционный способ написания чисел; в этом случае в нижнем ряду записывались «единицы», во втором снизу  «двадцатки», каждая единица третьего порядка равнялась 360 (число дней в году), четвертого порядка  7200 (360 X 20) и т. п.; использовался, согласно Ю. В. Кнорозову,

____

5. В. В. Струве. История древнего Востока. М., 1941, стр. 116.

[512]

также особый знак, указывающий на отсутствие цифр данного разряда, т. е. выполнявший функцию нуля 6.

Сильно сказался на развитии цифровых знаков переход к слоговым и звуковым системам. В этих системах возникло принципиальное различие между цифрами, которые оставались семантическими логограммами (идеограммами), и всеми остальными письменными знаками, получившими фонетическое (слоговое или звуковое) значение. В связи с этим, наряду с логографически-цифровой записью чисел начала широко применяться и фонетическая их запись (например, «6» и «шесть»). Это привело к обособлению цифр как специальных знаков. В свою очередь осознание цифр как особых знаков позволило придать и обычным письменным знакам (буквам) дополнительное логографически-цифровое значение, привело к (возникновению новых («алфавитных») цифровых систем.

Правда, наряду с алфавитными цифровыми системами (ионической греческой, славянской, армянской, грузинской и др.) продолжали создаваться системы прежнего неалфавитного типа (финикийская, сирийские, аттическая греческая, римская и др.), в которых для обозначения чисел применялись знаки, отличные от букв. Однако противопоставление цифровых логограмм буквенно-звуковым знакам сказалось и на этих системах, в частности привело к развитию в них позиционного принципа (см. ниже).

Из поздних неалфавитных цифровых систем ближе к древнейшим (египетской, критской и др.) стояла финикийская система и системы, возникшие на ее основе (сирийские и др.). Так же, как и в древнейших, особые знаки здесь существовали для единицы (вертикальные черточки), для 10 (горизонтальные черточки) и для 100; остальные числа получались по принципу сложения (повторения) знаков (единица), (десять) (сто). Однако наряду с десятичными в некоторых из этих систем существовали особые знаки для чисел (пять) и (двадцать), т. е. десятичный принцип дополнялся пятиричным и двадцатиричным. Кроме того, большие производные числа (например, сотни) получались не только по принципу сложения, но и по принципу умножения. Как та, так и другая особенность упростили написание больших чисел. Так, для числа 46, вместо четырехкратного повторения знака (десять) и шестикратного повторения знака (единицы), повторяли два раза знак (двадцать), один раз (пять) и один раз (единица); соответственно число 500 передавалось не пятью знаками (сто), а одним знаком (сто) с присоединением к нему знака (пять).

_____

6. Ю. В. Кнорозов. Письменность индейцев майя. М.Л., 1963, стр. 251252.

[513]

На основе сочетания десятичного и пятиричного принципов была построена также греческая аттическая цифровая система («геродианова»), возникшая около VI века (позже она была вытеснена ионической «алфавитной» цифровой системой). В аттической системе особые знаки существовали для чисел 1,5, 10, 50, 100, 500, 1000 и 10 000; для передачи этих чисел применялись начальные буквы соответствующих греческих имен числительных. Остальные числа .получались ос -принципу сложения.

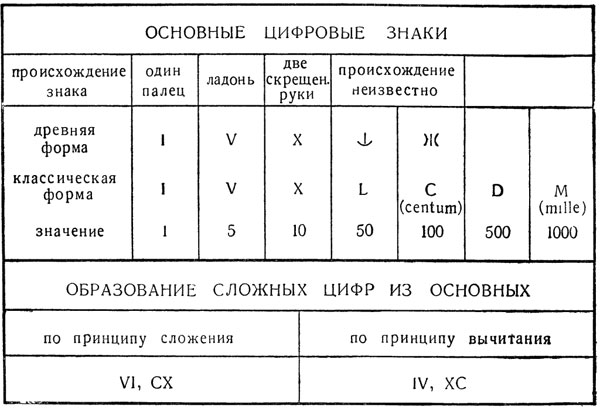
Аттическая система повлияла на «римскую» систему цифр, возникшую у этрусков около 500 г. до н. э. и затем заимствованную римлянами. Система эта (рис. 146) тоже сочетала десятичный и пятиричный принципы. Из семи основных знаков этой системы четыре (I, X, С, М) были построены на основе десятичного принципа; три (V, L, D)  на основе пятиричного. Отличалась римская система тем, что для получения остальных чисел в ней стал использоваться (примерно с XV в.) 7 не только принцип сложения (например, XI), /но и принцип вычитания (например, IX); это упрощало написание сложных чисел; так, число (четыре) писалось при помощи не четырех, а двух знаков (не 1111, а IV).

Форма римских цифр происходит от счета на пальцах и от словесного наименования чисел. По первому принципу построены цифры: I (один палец), V(ладонь с отставленным большим пальцем), X (две скрещенные руки); по второму  цифры С (первая буква слова centum  «сто») и М (первая буква слова mille «тысяча»); недостаточно ясно происхождение цифр L и D. В древнейших римских письменных памятниках (до нашей эры) цифра D (500) не встречалась, а для чисел 50, 100 и 1000 использовались иногда западно-греческие буквы, не вошедшие в латинский алфавит: для 50 (quinquaginto)  буква Ψ («пси», произносившаяся в западно-греческом письме, как kh); для 100  буква θ («тета»); для 1000 Φ («фи»); в связи с этим считают, что цифра D (500) получена как половина буквы φ («фи») применявшейся некогда для числа 1000, а новая форма цифр 50 и 100 возникла путем видоизменения их первоначальной формы 8. Римская система до XII-XIII веков была единственной цифровой системой в западноевропейских странах; впоследствии ее вытеснили более удобные «арабские» цифры.

Применение для получения производных чисел и сложения, и умножения либо сложения и вычитания оказалось возможным

_____

7. О. А. Добиаш-Рождественская. История письма в средние века. М Л., 1923, стр. 177.

8. И. М. Тройский. Историческая грамматика латинского языка. М., 1960, стр. 69.

[514]

146. Римская цифровая система

лишь в результате использования «позиционного принципа» (например, IV и VI). В свою очередь последовательное применение позиционного принципа стало возможным лишь вследствие осознания особого характера цифровых знаков, отличного от обычных знаков письма. А осознание особого характера цифр, как уже указывалось, смогло оформиться только тогда, когда основные знаки письма приобрели (в отличие от цифр) фонетическое значение; когда наряду с логографически-цифровой записью чисел, начала применяться фонетическая их запись.

В алфавитных цифровых системах в качестве цифровых знаков использовались буквы; при этом на цифровое (а не звуковое) значение букв указывала черточка, проставлявшаяся над буквой. Важнейшим отличием этих систем было большое количество разных цифровых знаков (обычно девять знаков для единиц, девять для десятков, девять для сотен и один знак для тысячи). Это упрощало написание чисел, позволяло обозначать любое число в пределах тысячи при ломощи одного-двух, максимум трех знаков (по принципу их сложения). Что касается больших чисел, то они получались по принципу умножения; это тоже упрощало их написание.

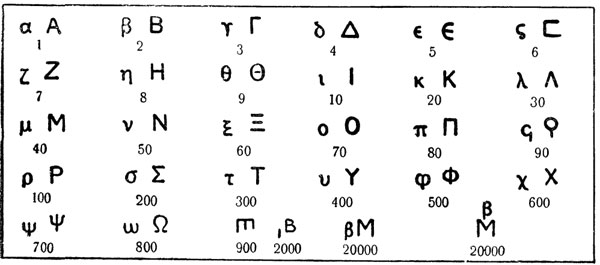
Так, в ионической греческой цифровой системе (рис. 147), возникшей около V века до н. э., в качестве основных знаков, служивших для обозначения единиц, десятков и сотен, были

[515]

147. Греческая (ионическая) цифровая система.

использованы 24 буквы классического греческого алфавита с добавлением трех букв («дигамма» - шесть, «коппа» - девяносто и «сампи» - девятьсот), вышедших из употребления. Тысячи обозначались теми же буквами с простановкой штриха внизу слева от буквы.

На основе и по образцу греческой были построены алфавитные цифровые системы других народов  славянские (кирилловская и глаголическая), армянская, грузинская.

В славянско-глаголической системе в качестве основных цифровых знаков были использованы первые 28 букв алфавита (см. рис. 117); в кириллице (рис. 117 и 148) цифровое значение получили, как правило, лишь буквы, заимствованные из греческого письма.

Алфавитные системы цифр были прогрессивным явлением, так как они упростили запись чисел. Однако это было достигнуто за счет увеличения ассортимента знаков; он приближался к 30.

Наиболее совершенная цифровая система, получившая позже название «арабской», была создана в Индии около V века.

До этого в Индии применялись системы цифр кхарошти и брахми. Система кхарошти была близка к финикийской и арамейской. В брахми числа 1, 2, 3 передавались соответствующим количеством горизонтальных черточек; для 4, 5, 6, 7, 8, 9, 10  существовали особые знаки. Применялся также позиционный принцип  десятки писались влево от единиц, сотни  влево от десятков. Около V века система брахми была переработана на основе последовательного применения принципов, проверенных всей историей развития цифр  десятичного, позиционного и принципа сложения, а также на основе использования знака «нуль».

В соответствии с десятичным и позиционным принципами в этой системе применяется только десять разных цифровых знаков  от

[516]

148. Славяно-кирилловская цифровая система. «Зело», сходная по форме с византийской «дигаммой», первоначально, видимо, обозначала только число 6 и лишь затем получила звуковое значение. Число 90 сперва обозначалось «коппой», позже  сходной с «коппой» буквой «червь». Для 900 применялась «сампи», затем  сходный с ней «юс малый», еще позже (возможно под влиянием глаголицы)  кирилловская «цы».

0 до 9. При этом значение каждого из них определяется не только его формой, но и местом, занимаемым им в ряду других цифр; так, цифры, расположенные в крайнем правом вертикальном ряду, обозначают единицы, во втором справа десятки, в третьем ряду сотни и т. д. Отсутствие числа соответствующего ряда (например, сотен) обозначается простановкой в соответствующем месте (например, между десятками и тысячами) знака «нуль». Согласно принципу сложения, все цифры, входящие в один горизонтальный ряд, складываются: так, запись 135 расшифровывается как 100 + 30 + 5. Десятичный принцип и принцип сложения использовались почти во всех цифровых системах. Поэтому наиболее важным и новым в индийской системе было последовательное применение позиционного принципа (в вавилонской, римской и других системах этот принцип применялся непоследовательно) и знака нуль (аналогичные знаки использовались в системах майя и вавилонской).

[517]

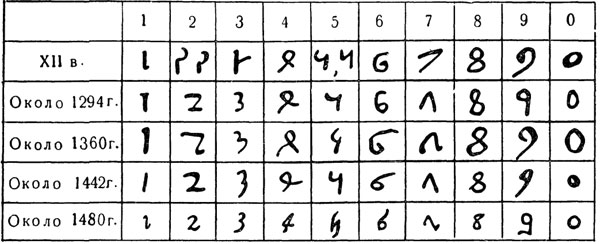
149. Эволюция формы арабских цифр

Индийская система цифр перешла к арабам, которые придали индийским цифрам иную форму; от арабов эта система (под названием «арабских цифр») распространилась по всей Европе. В Испании первые случаи использования «арабских» цифр относятся к X веку, в других странах Европы  к XII в.; первое описание арабских цифр дано в книге Леонардо из Пизы «Liber abaci» (1208 г.). Широкое применение арабских цифр в Западной Европе начинается со второй половины XV века. В России арабские цифры появляются в XIV-XV века, распространение получают с XVII века, а окончательно вытесняют из гражданской печати славянско-кирилловские цифры в XVIII веке, после введения гражданской азбуки. Первоначальная форма арабских цифр (см. рис. 149) была несколько иной (кроме цифр 1, 6, 7, 8, 9, 0), чем форма их у европейских народов. В настоящее время в близком к прежнему арабскому их начертанию эти цифры применяются в тех странах, которые пользуются арабской системой письма (Иран, Афганистан, Пакистан и др.).

Наряду с арабской ограниченное применение сохранила римская цифровая система; система эта используется для обозначения столетий, на циферблатах часов и в случаях сложной нумерации, когда одной арабской системы оказывается недостаточно (например, когда книга делится на главы, а главы на разделы); реже применяется для последней цели греческая цифровая система. В Китае до сих пор сохранили применение наряду с арабскими и римскими китайские цифры.

Крупнейшим усовершенствованием арабской системы цифр было изобретение .в конце XVI в, бельгийским ученым С. Стевенюм десятичных дробей9. После этого арабские цифры стали пригодны для десятичной позиционной записи любых как самых малых, так и самых больших чисел.

_____

9. S. Stevin. La Disme. Paris, 1856.

[518]

Цитируется по изд.: Истрин В.А. Возникновение и развития письма. М., 1965, с. 506-518.