Интуиционистская логика
ИНТУИЦИОНИСТСКАЯ ЛОГИКА – первоначально логика интуиционистской математики, получившая впоследствии более широкое применение. Неформально развивалась Л.Брауэром с 1907 г., первую интерпретацию, независимую от интуиционистской идеологии, дал А.Н.Колмогоров, первые формализации построили В.Гливенко и А.Гейтинг.
Язык интуиционистской логики совпадает с языком классической логики. Сохраняются и правила естественного вывода для всех связок, кроме отрицания. Для отрицания правило снятия двойного отрицания ослабляется до правила «Из лжи следует все, что угодно». В результате ослабляются возможности косвенного вывода – косвенно можно опровергать (по правилу reductio ad absurdum), но, вообще говоря, нельзя доказывать положительные суждения от противного.
В интуиционистской логике все связки независимы. Более того, для доказательства утверждения А достаточно пользоваться лишь формулами, не содержащими связок, отсутствующих в А. В интуиционистской логике нет стандартных (нормальных) форм, аналогичных классическим. Как правило, преобразования, связанные с законами формулировки отрицаний и приведения к предваренной форме, действуют лишь в одну сторону. Так, напр., верно Α∨Β⇒ (Α&Β), а (А&В) ⇒Α∨Β выполнено не всегда. Сильный исключенного третьего закон (tertium non datur) отвергается, но его слабая форма «А и его отрицание не могут быть одновременно ложны» (Α∨Α), сохраняется. Поэтому неправильно трактовать интуиционистскую логику как вводящую дополнительные истинностные значения, она скорее отвергает саму концепцию логических значений.
Интуиционистская логика обладает рядом выдающихся свойств в классе неклассических логик. Для нее выполнены теорема Крейга об интерполяции: «Если выводимо А⇒С, то можно построить формулу В, содержащую лишь термины, входящие и в А, и в С, такую, что выводимы А⇒В, В ⇒С» и теорема Бета об определимости: «Если в сигнатуре σ выделена подсишатура σ0, и термин Τ не принадлежит σ0, но сохраняет одно и то же значение для всех моделей теории Th, в которых совпадают значения терминов из σ0, то Τ определим через σ0 в теории Th.»
Эти две теоремы сохраняются лишь для малого числа неклассических логик. Более распространенным свойством является нормализуемость выводов, позволяющая в принципе устранить леммы из доказательств. Оно также выполнено для интуиционистской логики.
Выполнено для нее и свойство корректности относительно ∨ и ∃: если доказано А∨В, то доказано либо А, либо В; если доказано ∃хА(х), то для некоторого t доказано А(t). Данным свойством классическая логика не обладает. Интуиционистская логика – единственная логика среди континуума логик с тем же языком, что и классическая, для которой выполнены все эти свойства.
Таким образом, она может служить основой для содержательных математических теорий, поскольку в ней интуитивная определимость совпадает с формальной. Хотя множества теорем и доказательств интуиционистской логики по объему уже соответствующих множеств классической, последняя вкладывается в интуиционистскую. Первым такое погружение осуществил Гливенко. Таким образом, выразительные возможности интуиционистской логики сильнее классической. В свою очередь, К.Гёдель показал, что интуиционистская логика вкладывается в модальную логику S4. При этом погружении связки &, ∨, ∃ остаются без изменения, а на элементарные формулы и на результаты применения остальных связок навешивается модальность.
Интуиционистская логика не может быть описана никакой конечной системой логических значений, и, более того, для нее неестественно описание с помощью таблиц истинности (хотя счетнозначные таблицы истинности для нее существуют). Но она имеет несколько математических интерпретаций. Исторически первой была интерпретация А.Тарского. В ней значениями истинности для предикатов являются открытые подмножества топологического пространства. Значения &, ∨, ∃ определяются булевым образом. Значение А есть внутренность дополнения значения А. Это вызвано тем, что дополнение открытого множества часто не является открытым. Аналогично определяются значения А ⇒В и ∀xA(х). Напр., несправедливость A∨A можно продемонстрировать следующим образом: объединение открытого единичного круга и внутренности его дополнения дает не всю плоскость, а плоскость без единичной окружности.
Следующей интерпретацией была алгебраическая модель – алгебры Линденбаума-Тарского для интуиционистских теорий. Их называют псевдобулевыми алгебрами. Эти алгебры впервые были созданы для данной цели, но оказались распространенной и широко применимой структурой.
Параллельно с этим развивалась линия, ведущая начало от брауэровского содержательного смысла интуиционистской логики. Формулы истолковывались как задачи, логические связки – как преобразования задач, аксиомы – как задачи, для которых решения считаются известными, а правила вывода – как преобразования решений задач. Данные идеи систематизировал А.Н. Колмогоров. Каждой формуле А сопоставляется множество ее реализаций ®. Каждая реализация считается решением задачи, соответствующей А. Реализации элементарных формул задаются по определению. ®(А&В) = ®А × ®В, где ®(А&В) это пара реализаций <®А®В>; ®(А∨В) = ®А 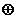 ®В, где ®(А∨В) – реализация А или В с указанием, какая из подзадач решена; ®A = 0̊⇔®А = ∅, где ®А – стандартный элемент, например О, при условии, что задача А неразрешима; ®∃хА(х) =
®В, где ®(А∨В) – реализация А или В с указанием, какая из подзадач решена; ®A = 0̊⇔®А = ∅, где ®А – стандартный элемент, например О, при условии, что задача А неразрешима; ®∃хА(х) = 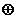 а∈U®A(α), где ®∃хА(х) – это пара из значения х0 и решения A(x0). Реализациями А ⇒ В являются эффективные функционалы из ®А в ®В. Реализациями ∀хА(х) являются эффективные функционалы, перерабатывающие каждое α ∈ U в реализацию Α(α).
а∈U®A(α), где ®∃хА(х) – это пара из значения х0 и решения A(x0). Реализациями А ⇒ В являются эффективные функционалы из ®А в ®В. Реализациями ∀хА(х) являются эффективные функционалы, перерабатывающие каждое α ∈ U в реализацию Α(α).
В данном определении остается не уточненным понятие эффективного функционала. Оно может уточняться по-разному, в частности, если взять в качестве эффективных функционалов все классические функции, то логика превращается в классическую. С.К.Клини построил первый точный вариант реализуемости, взяв в качестве эффективных операторов алгоритмы и кодируя программы алгоритмов натуральными числами, обходя таким образом сложности с операторами высших типов (клиниевская реализуемость). Он показал, что из доказательства в интуиционистской арифметике извлекается клиниевская реализация доказанной теоремы, и, таким образом, если мы доказали ∃хА(х), то имеется такое п, что доказано А(п). Это точно обосновало тезис Брауэра о том, что интуиционистские доказательства дают, в отличие от классических, построения.
Еще одна семантика интуиционистской логики берет начало от Бета и развита Крипке. Это – один из видов моделей Крипке. Множество миров – частично-упорядоченное множество (достаточно рассматривать дерево), истинность элементарных формул сохраняется при подъеме, универсумы не уменьшаются при подъеме, значения &, ∨, ∃определяются локально, w⊧A⊃B⇔∀v≥w (v⊧A⇒v⊧B), w ⊧A⇔∀v≥w (v ⊧ A), w ⊧∀x A(x) ⇔∀v ≥ w (∀a∈Uv ν ⊧A(a)), где v и w– это «переменные по мирам». Данные пункты практически повторяют на семантическом уровне гёделево погружение интуиционистской логики в S4. Модели Крипке изоморфны алгебраическим и топологическим моделям (порядок определяет псевдобулеву алгебру верхних отрезков множества миров и топологию, в которой окрестностями служат верхние отрезки).
Уникальным для неклассических логик является наличие у интуиционистской логики двух разнородных и несводимых друг к другу классов семантик: реализуемостей и моделей Крипке. Аналогия между доказательствами в интуиционистской логике и построениями усилена Н.В.Карри в его «Комбинаторной логике» (Combinatory Logic, 1968). Замкнутые типизированные выражения в комбішаторной логике изоморфны выводам в гильбертовской формулировке импликативного фрагмента интуиционистской логики. Замкнутые типизированные λ-термы изоморфны выводам в импликативном фрагменте естественного вывода. Изоморфизм между выводами и λ-термами пытались расширить на всю интуиционистскую логику, обобщая λ-исчисление. Но на этом пути стоит препятствие, указанное еще Брауэром и явно выделенное Н.А.Шаниным. Выводы в интуиционистской логике соединяют построения и их обоснования. В частности, построения, проделанные при выводе А, нельзя вычислять, поскольку они приведут к ошибке. Но подобным же действием могут обладать и другие импликации, в частности, закон транзитивности ∀xyz (А(х, у) &А(у, z) ⇒ А(х, z) Здесь может привести к нежелательным последствиям вычисление у. Такие объекты, которые нельзя или не нужно вычислять в программе, но нужно рассматривать для ее обоснования, ввел Г.С.Цейтин и назвал «призраками». Н.А.Шанин рассмотрел алгоритм конструктивной расшифровки, разбивающий формулу на задачу и обоснование решения, причем вторая часть могла доказываться классически. Его решение имеет место для рекурсивной реализуемости в теории, пополненной принципом Маркова: ∀х (А(х) ∨A(х)) & ∃xA(x) ⇒∃хА(х).
Содержательный смысл данного принципа раскрывается изречением «Ищите и обрящете»: если известны критерии проверки правильности решения и доказано его существование, то его может найти машина полным перебором. Н.Н.Непейвода дал алгоритм классификации объектов внутри произвольного вывода в интуиционистской логике, отделяющий действующие объекты и формулы от бездействующих, порождающих лишь обоснования и призраки.
Интуиционистскую логику пытались варьировать многими способами. Первой вариацией была минимальная логика Иогансона, получающаяся отбрасыванием ех falso sequitur quodlibet. Как оказалось, в прикладных теориях интуиционистское отрицание тем не менее моделируется (напр., в любой теории, содержащей натуральные числа, как А ⇒0 = 1). Но минимальная логика, как и интерпретация Колмогорова, высветила аномальный статус отрицания в интуиционистской логике. Это – единственная связка, не требующая никакого построения.
В связи с этим Грис предложил симметрическую интуиционистскую логику, в которой истина и ложь определяются одновременно и равноправно. В симметрической интуиционистской логике сохраняются обычные правила формулировки отрицаний классической логики, и в ее натуральном варианте они даже постулируются в качестве правил вывода. Отрицание в ней обычно обозначается ~А и называется «сильным отрицанием», или «конструктивным опровержением». Оно интерпретируется как задача на построение контрпримера к А. Симметрическая интуиционистская логика детально исследована в монографии И.Д.Заславского.
Ю.М.Медведев предложил рассматривать логику финитных задач и заметил, что, если функционалы всюду определены, то формула (А ⇒ В ∨C) ⇒ ((A ⇒ Β)∨( Α ⇒ C)) реализуема (реализация А стандартна, и ее можно подставить в функционал, чтобы выявить единственного кандидата на решение среди В, C). Вслед за этим начали рассматриваться многочисленные суперинтуиционистские логики, получающиеся расширением интуиционистской логики некоторыми схемами аксиом. Почти все они либо влекут закон исключенного третьего в прикладных теориях, либо не удовлетворяют теореме Крейга об интерполяции и теореме Бета. Так что интуиционистская логика занимает уникальное место в классе неклассических логик, не только как старейшая из них, но и как концептуально целостная система.
Н. Н. Непейвода
Новая философская энциклопедия. В четырех томах. / Ин-т философии РАН. Научно-ред. совет: В.С. Степин, А.А. Гусейнов, Г.Ю. Семигин. М., Мысль, 2010, т. II, Е – М, с. 138-140.
Литература:
Brouwer L. Е. J. Over de grondslagen der wiskunde (Об основаниях знания). Amst.—Lpz., 1907; Brouwer L. E.J. De onbetrouwbaarheid der logische principes (О недостоверности логических принципов). — Ti- jdsehz voor Wijsbegeerte, v. 2, 1908; Kolmogoroff A. Zur Deutung der intuitionistischen Logik. — «Math. Zeitschrift», v. 35,1932 (рус. пер.: К толкованию интуиционистской логики. — В кн.: Колмогоров А. Н. Избр. тр., Математика и механика. М., 1985); HeytingA. Die formalen Regeln der Intuitionistischen Logik. — Sitz. Der Preus. Akad., Phys.-mathematische Klasse. В., 1930; Tarski A. Der Aussagenkalkul und die Topologie.— «Fun- damenta Mathematicae», v. 31, 1938; Curry H. B. Combinatory Logic, v. 2. N. Y., 1968; Шанин H. А. О конструктивном понимании математических суждений,— В кн.: Труды Математического института им. В. А. Стеклова, т. 52, 1958; Непейвода Н. Н. О построении правильных программ. — «Вопросы кибернетики», т. 46,1978, с. 88—122.