Разрешения проблема
РАЗРЕШЕНИЯ ПРОБЛЕМА – возникла в связи с осознанием невозможности провести некоторые построения дозволенными методами. Первыми примерами неразрешимых задач явились решение в радикалах уравнений выше четвертой степени и невозможность провести некоторые построения циркулем и линейкой.
Общая формулировка проблемы разрешения следующая: дан класс методов Ф, дан класс проблем Р. Можно ли найти единый метод f ∈Φ (разрешающий метод), позволяющий решить каждую из проблем Р, для которой в принципе существует решение?
Часто в текстах по логике и математике рассматривается более частная формулировка проблемы разрешения, называемая алгоритмической разрешимостью, в которой разрешающий метод должен быть алгоритмом, т.е. класс методов Φ фиксируется и считается множеством алгоритмов. Исторически алгоритмическая неразрешимость была первым явно выделенным случаем общей проблемы разрешения. В последнее время в связи с осознанием разницы между теоретической и практической вычислимостью появилась третья формулировка, когда разрешающий метод – не просто алгоритм, а алгоритм ограниченной сложности. Напр., линейная разрешимость – разрешимость программой, вычислимая за линейное время относительно длины исходных данных, NP-полная проблема – проблема, разрешимая лишь программой полного перебора.
Примерами в разной степени неразрешимых проблем являются:
построение модели любой непротиворечивой классической теории – неразрешима однозначно определенными (без аксиомы выбора) теоретико-множественными функционалами; проверка истинности формул арифметики либо (соответствия) программ их спецификации – неразрешима средствами формальных теорий с алгоритмически заданным множеством аксиом;
проверка доказуемости в формальной арифметике или в классической логике предикатов – алгоритмически неразрешима; задача нормализации выводов в логике предикатов – неразрешима примитивно-рекурсивными алгоритмами;
задача перестройки естественного вывода в резолюционный – неразрешима алгоритмами, делающими не более
22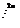 }(k раз)
}(k раз)
шагов, где n – длина вывода, k – любое фиксированное число; проверка тавтологичности формул классической логики высказываний – переборно разрешима, но неразрешима менее чем переборными алгоритмами.
Заметим, что неразрешимость проблемы означает лишь отсутствие единого метода, хотя в каждом конкретном случае ее можно пытаться решать, если решение не претендует на слишком большую общность. В последнее время выявилось общее свойство частных решений неразрешимых проблем: по мере расширения класса решаемых задач сложность методов с некоторого момента быстро растет, а эффективность столь же быстро убывает.
Точно так же результат о достаточно простой разрешимости проблемы может оказаться дезориентирующим, если эта достаточная простота достигается лишь на очень больших объектах, а для малых все равно приходится практически действовать перебором. Примером здесь может служить классическая задача о раскраске карт четырьмя цветами.
Сведение к неразрешимым проблемам стало столь же мощным методом установления некорректности задач либо решений, каким является в физике сведение к возможности построить вечный двигатель. Напр., того, кто написал программу, ищущую зацикливание в других программах, не будут слушать, если он сам не предоставит примеры, когда его программа не работает либо работает неправильно.
Неразрешимость проблемы разложения числа на простые множители достаточно простым алгоритмом стала основой современной теории надежных индивидуальных шифров.
Одним из методов решения неразрешимых проблем является переход к вероятностным алгоритмам разрешения и к квантовым вычислениям. Показано, что для многих переборных задач есть быстрые алгоритмы, решающие их со сколь угодно близкой к 1 заранее заданной вероятностью.
Н.Н. Непейвода
Новая философская энциклопедия. В четырех томах. / Ин-т философии РАН. Научно-ред. совет: В.С. Степин, А.А. Гусейнов, Г.Ю. Семигин. М., Мысль, 2010, т. III, Н – С, с. 402-403.